Question

How many zero pairs must be added to the function

f(x) = x2 – 6x + 1 in order to begin writing the function in vertex form?

Answer 1

(3,-8) that the answer

Answer 2

There is only one zero pair added i.e. 9.

Explanation:

Given : Function
`f(x)=x^2-6x+1`

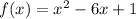
To find : How many zero pairs must be added to the function in order to begin writing the function in vertex form?

Solution :

Converting the given function into vertex form,

`f(x)=x^2-6x+1`

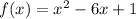
Adding and subtracting square of 3,

`f(x)=x^2-6x+(3)^2-(3)^2+1`

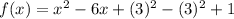
Square form as
`a^2-2ab+b^2=(a-b)^2`

`f(x)=(x-3)^2-9+1`

`f(x)=(x-3)^2-8`

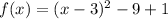
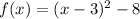
So, The required vertex form is
`f(x)=(x-3)^2-8`

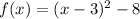
There is only one zero pair added i.e. 9.