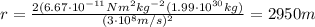Answer:
2950 m
Step-by-step explanation:
The radius to which the sun must be compressed to become a black hole is equal to its Schwarzschild radius, which is given by the formula:

where
G is the gravitational constant
M is the mass of the star
c is the speed of light
For the Sun, its mass is
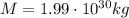
Therefore, its Schwarzschild radius is