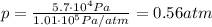Question

Suppose the gas resulting from the sublimation of 1.00 g carbon dioxide is collected over water at 25.0◦c into a 1.00 l container. What is the total pressure in the container? Express your answer in atmospheres.

Answer 1

0.56 atm

Step-by-step explanation:

First of all, we need to find the number of moles of the gas.

We know that

m = 1.00 g is the mass of the gas

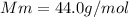`Mm=44.0 g/mol` is the molar mass of the carbon dioxide

So, the number of moles of the gas is

`n=(m)/(M_m)=(1.00 g)/(44.0 g/mol)=0.023 mol`

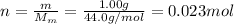
Now we can find the pressure of the gas by using the ideal gas equation:

`pV=nRT`

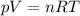
where

p is the pressure

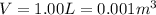`V=1.00 L = 0.001 m^3` is the volume

n = 0.023 mol is the number of moles

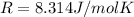`R=8.314 J/mol K` is the gas constant

`T=25.0^(\circ)+273=298 K` is the temperature of the gas

Solving the equation for p, we find

`p=(nRT)/(V)=((0.023 mol)(8.314 J/mol K)(298 K))/(0.001 m^3)=5.7 \cdot 10^4 Pa`

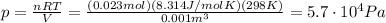
And since we have

`1 atm = 1.01\cdot 10^5 Pa`

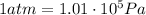
the pressure in atmospheres is

`p=(5.7\cdot 10^4 Pa)/(1.01\cdot 10^5 Pa/atm)=0.56 atm`