Question

Expectant mothers many times see their unborn child for the first time during an ultrasonic examination. In ultrasonic imaging, the blood flow and heartbeat of the child can be measured using an echolocation technique similar to that used by bats. For the purposes of these questions, please use 1500 m/s as the speed of sound in tissue. I need help with part B and C

PART A. To clearly see an image, the wavelength used must be at most 1/4 of the size of the object that is to be imaged. What frequency is needed to image a fetus at 8 weeks of gestation that is 1.6 cm long? I got 380 kHz for part A

A. 380 kHz

B. 3.8 kHz

C. 85 kHz

D. 3.8 MHz

PART B.Blood flow rates in the umbilical cord can be found by measuring the Doppler shift of the ultrasound signal reflected by the red blood cells. If the source emits a frequency f, what is the measured reflected frequency fR? Assume that all of the red blood cells move directly toward the source. Let c be the speed of sound in blood and v be the speed of the red blood cells.

A. f(c+v)/v−c

B. f(c+v)/c−v

C. f(c+v)/c

D. f(c−v)/v+c

PART C. Ultrasonic imaging is made possible due to the fact that a sound wave is partially reflected whenever it hits a boundary between two materials with different densities within the body. The percentage of the wave reflected when traveling from material 1 into material 2 is R=(ρ1−ρ2ρ1+ρ2)2. Knowing this, why does the technician apply ultrasound gel to the patient before beginning the examination?

A. The gel has a density similar to that of skin, so very little of the incident ultrasonic wave is lost by reflection.

B. The gel allows the instrument to slide more easily against the patient.

C. The gel provides a calibration density.

D. The sound waves do not dissipate through the gel.

Answer 1

A) A. 380 kHz

To clerly see the image of the fetus, the wavelength of the ultrasound must be 1/4 of the size of the fetus, therefore

`\lambda=(1)/(4)(1.6 cm)=0.4 cm=0.004 m`

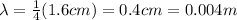
The frequency of a wave is given by

`f=(v)/(\lambda)`

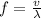
where

v is the speed of the wave

`\lambda` is the wavelength

For the ultrasound wave in this problem, we have

v = 1500 m/s is the wave speed

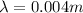`\lambda=0.004 m` is the wavelength

So, the frequency is

`f=(1500 m/s)/(0.004 m)=3.75\cdot 10^5 Hz=375 kHz \sim 380 kHz`

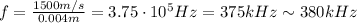
B) B. f(c+v)/c−v

The formula for the Doppler effect is:

`f'=(v\pm v_r)/(v\pm v_s)f`

where

f' is the apparent frequency

v is the speed of the wave

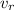`v_r` is the velocity of the receiver (positive if the receiver is moving towards the source, negative if it is moving away from the source)

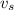`v_s` is the speed of the source (positive if the source is moving away from the receiver, negative if it is moving towards the receiver)

f is the original frequency

In this problem, we have two situations:

- at first, the ultrasound waves reach the blood cells (the receiver) which are moving towards the source with speed

`v_r = +v` (positive)

- then, the reflected waves is "emitted" by the blood cells (the source) which are moving towards the source with speed

`v_s = -v`

also

v = c = speed of sound in the blood

So the formula becomes

`f'=(c + v)/(v - v_s)f`

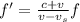
C. A. The gel has a density similar to that of skin, so very little of the incident ultrasonic wave is lost by reflection

The reflection coefficient is

`R=((Z_1 -Z_2)^2)/((Z_1+Z_2)^2)`

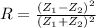
where Z1 and Z2 are the acoustic impedances of the two mediums, and R represents the fraction of the wave that is reflected back. The acoustic impedance Z is directly proportional to the density of the medium,
`\rho`.

In order for the ultrasound to pass through the skin, Z1 and Z2 must be as close as possible: therefore, a gel with density similar to that of skin is applied, in order to make the two acoustic impedances Z1 and Z2 as close as possible, so that R becomes close to zero.