Answer:
x = 50.05549481°
x ≈ 50.06°
Explanation:
The diagram makes a right-angles triangle; therefore we can use trigonometry.
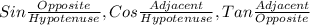
The hypotenuse is the side opposite the right angle - 150
The oppositite is the side opposite the angle in question - 115
The angle in question - x
We will use the formula:
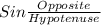
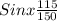
x = 50.05549481°
This is often rounded to 2 decimal places
x ≈ 50.06°