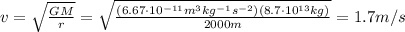Question

A spherical asteroid of average density would have a mass of 8.7×1013kg if its radius were 2.0 km. 1. If you and your spacesuit had a mass of 110 kg, how much would you weigh when standing on the surface of this asteroid? Express your answer to two significant figures and include appropriate units. 2. If you could walk on the surface of this asteroid, what minimum speed would you need to launch yourself into an orbit just above the surface of the asteroid? Express your answer to two significant figures and include appropriate units.

Answer 1

1. 0.16 N

The weight of a man on the surface of asteroid is equal to the gravitational force exerted on the man:

`F=G(Mm)/(r^2)`

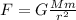
where

G is the gravitational constant

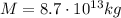`M=8.7\cdot 10^(13)kg` is the mass of the asteroid

m = 100 kg is the mass of the man

r = 2.0 km = 2000 m is the distance of the man from the centre of the asteroid

Substituting, we find

`F=(6.67\cdot 10^(-11)m^3 kg^(-1) s^(-2))((8.7\cdot 10^(13) kg)(110 kg))/((2000 m)^2)=0.16 N`

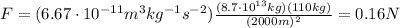
2. 1.7 m/s

In order to stay in orbit just above the surface of the asteroid (so, at a distance r=2000 m from its centre), the gravitational force must be equal to the centripetal force

`m(v^2)/(r)=G(Mm)/(r^2)`

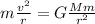
where v is the minimum speed required to stay in orbit.

Re-arranging the equation and solving for v, we find:

`v=\sqrt{(GM)/(r)}=\sqrt{((6.67\cdot 10^(-11) m^3 kg^(-1) s^(-2))(8.7\cdot 10^(13) kg))/(2000 m)}=1.7 m/s`