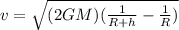Question

An object of mass m is dropped from height h above a planet of mass M and radius R .

Find an expression for the object's speed as it hits the ground.
Express your answer in terms of the variables m,M,h,R and appropriate constants.

v= _____

Answer 1

`v=\sqrt{(2GM)((1)/(R+h)-(1)/(R))}`

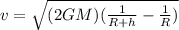
Step-by-step explanation:

The initial mechanical energy of the object, when it is suspended at a height h above the planet of radius R and mass M, is just gravitational potential energy, so

`E_i = U_i = (GMm)/(R+h)`

When the object reaches the ground, its mechanical energy is now sum of its kinetic energy Kf and its new gravitational potential energy Uf:

`E_f = K_f+U_f = (1)/(2)mv^2 + (GMm)/(R)`

Since the mechanical energy is conserved, we can write

Ei = Ef

So we can write

from which we can find an expression for v, the speed of the object when it hits the ground:

`v=\sqrt{(2GM)((1)/(R+h)-(1)/(R))}`