Question

The Earth revolves around the Sun once a year at an average distance of 1.50×1011m. Find the orbital radius that corresponds to a "year" of 180 day

Answer 1

`9.4\cdot 10^(10) m`

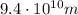
Step-by-step explanation:

We can solve the problem by using Kepler's third law, which states that the ratio between the cube of the orbital radius and the square of the orbital period is constant for every object orbiting the Sun. So we can write

`(r_a^3)/(T_a^2)=(r_e^3)/(T_e^2)`

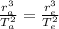
where

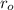`r_o` is the distance of the new object from the sun (orbital radius)

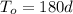`T_o=180 d` is the orbital period of the object

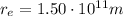`r_e = 1.50\cdot 10^(11) m` is the orbital radius of the Earth

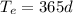`T_e=365 d` is the orbital period the Earth

Solving the equation for
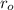`r_o`, we find

`r_o = \sqrt[3]{(r_e^3)/(T_e^2)T_o^2} =\sqrt[3]{((1.50\cdot 10^(11)m)^3)/((365 d)^2)(180 d)^2}=9.4\cdot 10^(10) m`