Answer:
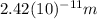
Step-by-step explanation:
The de Broglie wavelength
 is given by the following formula:
is given by the following formula:
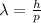 (1)
(1)
Where:
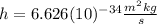 is the Planck constant
is the Planck constant
 is the momentum of the atom, which is given by:
is the momentum of the atom, which is given by:
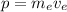 (2)
(2)
Where:
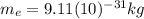 is the mass of the electron
is the mass of the electron
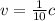 is the velocity of the electron (we are told it is 1/10 the speed of light
is the velocity of the electron (we are told it is 1/10 the speed of light
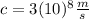 )
)
This means equation (2) can be written as:
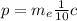 (3)
(3)
Substituting (3) in (1):
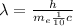 (4)
(4)
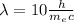 (5)
(5)
Now, we only have to find
 :
:
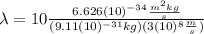 (6)
(6)
Finally:
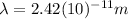 >>> This is the de Broglie wavelength of an electron.
>>> This is the de Broglie wavelength of an electron.