Question

Monochromatic light with a wavelength of 6.4 E -7 meter passes through two narrow slits, producing an interference pattern on a screen 4.0 meters away. The first order bright band lines are 2.0 E -2 meters away from the central bright maxima.

What is the distance between the slits?

Answer 1

1.3 E -4 m should be correct.

Answer 2

The distance between the slits is
`1.3*10^(-4)\ m`.

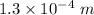Step-by-step explanation:

Given that,

The wavelength of the monochromatic light
`\lambda= 6.4*10^(-7)\ m`

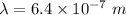
Distance = 4.0 m

Width
`\beta = 2.0*10^(-2)`

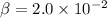
Using formula of the distance between the slits

`d = (n\lambda D)/(x)`

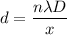
Where, x = distance from central fringe

D = Distance between the slit and screen

d = distance between the slits

n = number of order

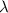`\lambda`=wavelength

Put the value into the formula

`d=(1*6.4*10^(-7)*4.0)/(2.0*10^(-2))`

`d =1.3*10^(-4)\ m`

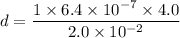
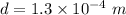
Hence, The distance between the slits is
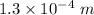`1.3*10^(-4)\ m`.