Question

A starship blasts past the earth at 2.0*10^8 m/s .Just after passing the earth, the starship fires a laser beam out its back of the starship.With what speed does the laser beam approach the earth?Express your answer using two significant figures.

Answer 1

The laser beam approaches the Earth at a speed of 5.0*10⁸ m/s.

Step-by-step explanation:

To find the speed at which the laser beam approaches the Earth, we need to consider the concept of relative velocity. Relative velocity is the velocity of an object with respect to another object. In this case, the laser beam is fired out of the back of the starship, which is already moving at a speed of 2.0*10⁸ m/s relative to the Earth.

Since the laser beam is being fired in the same direction as the starship's motion, the speed at which the laser beam approaches the Earth will be the sum of the starship's speed and the speed of the laser beam.

Therefore, the speed of the laser beam approaching the Earth will be 2.0*10⁸ m/s (starship's speed) + 3.0*10⁸ m/s (speed of light) = 5.0*10⁸ m/s.

Answer 2

at the speed of light (
`c=3.0\cdot 10^8 m/s`)

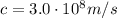Step-by-step explanation:

The second postulate of the theory of the special relativity from Einstein states that:

"The speed of light in free space has the same value c in all inertial frames of reference, where
`c=3.0\cdot 10^8 m/s`"

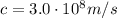This means that it doesn't matter if the observer is moving or not relative to the source of ligth: he will always observe light moving at the same speed, c.

In this problem, we have a starship emitting a laser beam (which is an electromagnetic wave, so it travels at the speed of light). The startship is moving relative to the Earth with a speed of 2.0*10^8 m/s: however, this is irrelevant for the exercise, because according to the postulate we mentioned above, an observer on Earth will observe the laser beam approaching Earth with a speed of
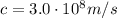`c=3.0\cdot 10^8 m/s`.