Question

A real object is 10.0 cm to the left of a thin, diverging lens having a focal length of magnitude 16.0 cm. What is the location of the image?A)6.15 cm to the left of the lensB)26.7 cm to the right of the lensC)6.15 cm to the right of the lensD)6.00 cm to the right of the lensE)26.7 cm to the left of the lens

Answer 1

A)6.15 cm to the left of the lens

Step-by-step explanation:

We can solve the problem by using the lens equation:

`(1)/(q)=(1)/(f)-(1)/(p)`

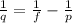
where

q is the distance of the image from the lens

f is the focal length

p is the distance of the object from the lens

In this problem, we have

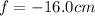`f=-16.0 cm` (the focal length is negative for a diverging lens)

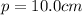`p=10.0 cm` is the distance of the object from the lens

Solvign the equation for q, we find

`(1)/(q)=(1)/(-16.0 cm)-(1)/(10.0 cm)=-0.163 cm^(-1)`

`q=(1)/(-0.163 cm^(-1))=-6.15 cm`

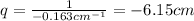
And the sign (negative) means the image is on the left of the lens, because it is a virtual image, so the correct answer is

A)6.15 cm to the left of the lens