Question

Help Me Please!!!

The following picture is a square pyramid where AE= 6√2 cm and ∠EAB = 45°.


Find the surface area of the pyramid. (Make sure you include formulas and numbers in the formulas as part of

your solution. Also, include units in your final answer)

Answer 1

The surface area is
`288\ cm^(2)`

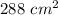
Explanation:

we know that

The surface area of the square pyramid is equal to the area of the square base plus the area of its four triangular lateral faces

so

`SA=b^(2) +4[((1)/(2)) (b)(h)]`

where

b is the length side of the square base

h is the height of each lateral triangular face

we know that

`(b)/(2)=h` -----> by angle of 45 degrees

`sin(45\°)=(h)/(6√(2))`

`h=6√(2)(sin(45\°)`

`h=6\ cm`

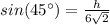
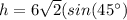
Find the value of b

`b=2h=2(6)=12\ cm`

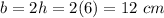
Find the surface area

`SA=12^(2) +4[((1)/(2)) (12)(6)]=288\ cm^(2)`