Question

A student determined that the area of the segment of c shown above is Asegment = 137.71 ft2. The student's work is shown below. Evaluate the student’s answer.

Answer 1

Option D. The student did not use the correct formula to calculate the area of the segment

Explanation:

step 1

Find the area of the isosceles triangle

Applying the law of sines

`A=(1)/(2)(12^(2))sin(60\°)=62.35\ ft^(2)`

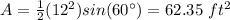
step 2

Find the area of the sector

The area of the sector is 1/6 of the area of the circle

so

`A=\pi r^(2)/6`

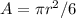
substitute the value

`A=(3.14)(12)^(2)/6=75.36\ ft^(2)`

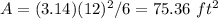
step 3

Find the area of the segment

The area of the segment is equal to the area of sector minus the area of triangle

`A=75.36\ ft^(2)-62.35\ ft^(2)=13.01\ ft^(2)`

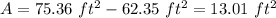
therefore

The student did not use the correct formula to calculate the area of the segment