Given:
The function is
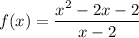
To find:
The vertical asymptote and oblique asymptote.
Solution:
We have,
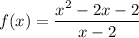
To find vertical asymptote, equate denominator equal to 0.
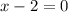
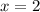
So, the vertical asymptote is
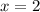 .
.
In the given function degree of numerator is greater than denominator so, their is an oblique asymptote. To find oblique asymptote divide the numerator by denominator.
Dividing
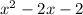 by
by
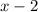 using synthetic division, we get
using synthetic division, we get
2 | 1 -2 -2
2 0
--------------------------
1 0 -2
-------------------------
Here, starting elements of bottom row represent coefficient of quotient and last element of bottom row represents the remainder.
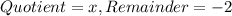
Since, quotient is x, therefore, the oblique asymptote is
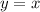 .
.
Therefore, the correct option is B.