Answer: The correct option is
(C) 7 units left.
Step-by-step explanation: We are given to select the correct description of the translation of graph y = |x| to obtain the graph of y = |x + 7|.
We know that
if the parent absolute function y = |x| is shifted a units to the left, then the new function is written as
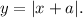
The given translated function is y = |x + 7|.
It describes that the function y = |x| is shifted 7 units to the left.
Thus, the correct description is
7 units left.
Option (C) is CORRECT.