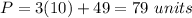Answer:
Part a) The value of x is 10
Part b) The perimeter of triangle JKL is
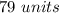
Explanation:
Part a) Find the value of x
we know that
The Triangle Proportionality Theorem, states that if a line parallel to one side of a triangle intersects the other two sides of the triangle, then the line divides these two sides proportionally
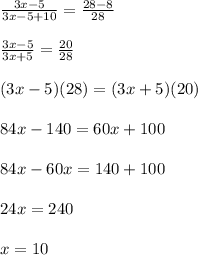
Part b) we know that
The perimeter of triangle JKL is equal to
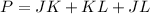
substitute the values
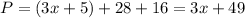
substitute the value of x