Question

A ball is thrown into the air from a height of 4 feet at time t = 0. The function that models this situation is h(t) = -16t2 + 63t + 4, where t is measured in seconds and h is the height in feet.

a) What is the height of the ball after 3 seconds?
b) What is the maximum height of the ball? Round to the nearest foot.
c) When will the ball hit the ground?
d) What domain makes sense for the function?

please show ur work !!!

Answer 1

Part a) The height of the ball after 3 seconds is
`49\ ft`

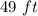
Part b) The maximum height is 66 ft

Part c) The ball hit the ground for t=4 sec

Part d) The domain of the function that makes sense is the interval

[0,4]

Explanation:

we have

`h(t)=-16t^(2) +63t+4`

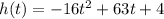
Part a) What is the height of the ball after 3 seconds?

For t=3 sec

Substitute in the function and solve for h

`h(3)=-16(3)^(2) +63(3)+4=49\ ft`

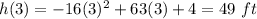
Part b) What is the maximum height of the ball? Round to the nearest foot.

we know that

The maximum height of the ball is the vertex of the quadratic equation

so

Convert the function into a vertex form

`h(t)=-16t^(2) +63t+4`

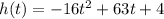
Group terms that contain the same variable, and move the constant to the opposite side of the equation

`h(t)-4=-16t^(2) +63t`

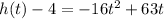
Factor the leading coefficient

`h(t)-4=-16(t^(2) -(63/16)t)`

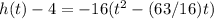
Complete the square. Remember to balance the equation by adding the same constants to each side

`h(t)-4-16(63/32)^(2)=-16(t^(2) -(63/16)t+(63/32)^(2))`

`h(t)-(67,600/1,024)=-16(t^(2) -(63/16)t+(63/32)^(2))`

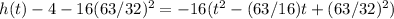
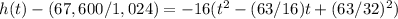
Rewrite as perfect squares

`h(t)-(67,600/1,024)=-16(t-(63/32))^(2)`

`h(t)=-16(t-(63/32))^(2)+(67,600/1,024)`

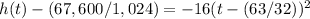
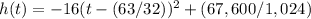
the vertex is the point (1.97,66.02)

therefore

The maximum height is 66 ft

Part c) When will the ball hit the ground?

we know that

The ball hit the ground when h(t)=0 (the x-intercepts of the function)

so

`h(t)=-16t^(2) +63t+4`

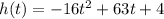
For h(t)=0

`0=-16t^(2) +63t+4`

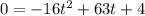
using a graphing tool

The solution is t=4 sec

see the attached figure

Part d) What domain makes sense for the function?

The domain of the function that makes sense is the interval

[0,4]

All real numbers greater than or equal to 0 seconds and less than or equal to 4 seconds

Remember that the time can not be a negative number