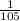Answer:
Explanation:
We have 15 diesel engines, from which 13 are okay, and 2 are defected. Since there are 15 engines and 13 will be chosen two ship in the continer, the possibe number of outcomes is:
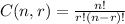
Where n = 15 and r=11.
Substituting, we find that:
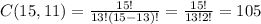
Now we need to find the probability of choosing 13 effective engines and 0 defective engines, which is given by:
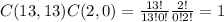
The probability of shipping the container is: