Question

Consider m = y2 - y1/ x2 - x1 . Which x1 and x2-values would determine that the line is vertical? Justify your answer

Answer 1

`x_2=x_1`

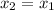
Explanation:

We were given the slope formula;

`m=(y_2-y_1)/(x_2-x_1)`

This line is vertical if the denominator is zero.

That is when
`x_2-x-1=0`

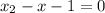
This implies that;

`x_2=x_1`

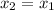
Justification;

When
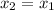`x_2=x_1`, then, the line passes through;

`(x_1,y_1)` and
`(x_1,y_2)`

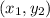
The slope now become

`m=(y_2-y_1)/(x_1-x_1)=(y_2-y_1)/(0)`

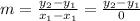
The equation of the line is

`y-y_1=(y_2-y_1)/(0)(x-x_1)`

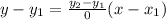
This implies that;

`0(y-y_1)=(y_2-y_1)(x-x_1)`

`0=(y_2-y_1)(x-x_1)`

`(0)/(y_2-y_1)=(x-x_1)`

`0=(x-x_1)`

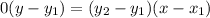
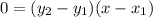
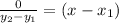
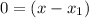
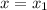`x=x_1`... This is the equation of a vertical line.