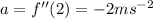Answer:
a) see attachment
b)
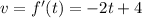
c)
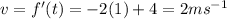
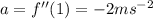
d)
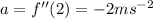
Explanation:
The position function of the object is given by;

a. The position function can be rewritten as;
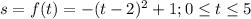
This the graph of
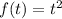 reflected in the x-axis,and shifted right 2 units, up 1 unit.
reflected in the x-axis,and shifted right 2 units, up 1 unit.
The graph is shown in the attachment.
b) The velocity function is given by;
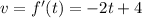
This is a straight line with slope -2 and y-intercept, 4.
The graph is shown in the attachment.
c) The velocity at t=1 is
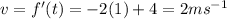
The acceleration is given by;
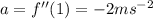
d) When the velocity is zero, we have;
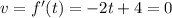
This implies that;
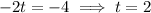
When t=2,