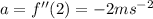Question

Suppose the position of an object moving horizontally after t seconds is given by the following functions s=f(t), s equals f , open t close , comma where s is measured in feet, with s>0 s greater than 0 corresponding to positions right of the origin.a. Graph the position function.b. Find and graph the velocity function. When is the object stationary, moving to the right, and moving to the left?c. Determine the velocity and acceleration of the object at t=1. t equals 1 .d. Determine the acceleration of the object when its velocity is zero.e. On what intervals is the speed increasing?f(t)= -t^2 +4t-3;0<=t<=5

Answer 1

a) see attachment

b)
`v=f'(t)=-2t+4`

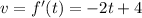
c)
`v=f'(t)=-2(1)+4=2ms^(-1)`

`a=f''(1)=-2ms^(-2)`

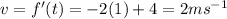
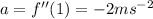
d)
`a=f''(2)=-2ms^(-2)`

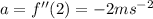
Explanation:

The position function of the object is given by;

`s=f(t)=-t^2+4t-3;0\leq t\leq 5`

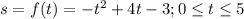
a. The position function can be rewritten as;

`s=f(t)=-(t-2)^2+1;0\leq t\leq 5`

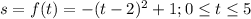
This the graph of
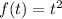`f(t)=t^2` reflected in the x-axis,and shifted right 2 units, up 1 unit.

The graph is shown in the attachment.

b) The velocity function is given by;

`v=f'(t)=-2t+4`

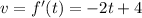
This is a straight line with slope -2 and y-intercept, 4.

The graph is shown in the attachment.

c) The velocity at t=1 is

`v=f'(t)=-2(1)+4=2ms^(-1)`

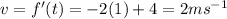
The acceleration is given by;

`a=f''(1)=-2ms^(-2)`

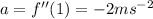
d) When the velocity is zero, we have;

`v=f'(t)=-2t+4=0`

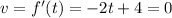
This implies that;

`-2t=-4\implies t=2`

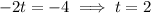
When t=2,

`a=f''(2)=-2ms^(-2)`