Answer:
Option A is correct.
Explanation:
Vertex of triangle are marked in attached pic.
So, we are given that ∠A = 95° , ∠B = 35° and c = 14 cm
We use law of sines.
which has following expression,
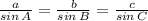
∠A + ∠B + ∠C = 180° (Angle sum property of triangle)
95 + 35 + ∠C = 180
∠C = 180 - 130
∠C = 50°
Now using Law of sines,

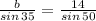

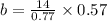

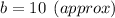
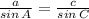

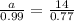
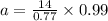
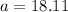
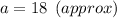
Now using area of triangle by herons formula,
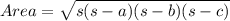
Semi perimeter, s =
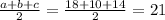
So we have,
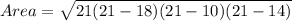
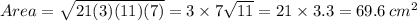
Since there is approximation in above calculated values, We select ans nearest to calculated one.
Therefore, Option A is correct.