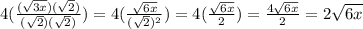Question

Simplify 4sqrt of (3/2x)

Answer 1

Answer:
`2√(6x)`

Explanation:

The expression
`4\sqrt{(3)/(2)x}` can be written as:

`4((√(3x))/(√(2)))`

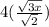
Therefore, to simplify the expression you need to Rationalize the denominator to get rid the radical
`√(2)`:

Then, you must multiply the numerator and the denominator by
`√(2)`.

Remember the following:

`(√(a))^(2)=a`

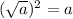
Also remember that:

`\sqrt[n]{a}*\sqrt[n]{b}=\sqrt[n]{ab}`

Therefore, you get:

`4(((√(3x))(√(2)))/((√(2))(√(2))))=4((√(6x))/((√(2))^2))=4((√(6x))/(2))=(4√(6x))/(2)=2√(6x)`