Question

Find the indicated limit, if it exists. (2 points) limit of f of x as x approaches 2 where f of x equals x plus 3 when x is less than 2 and f of x equals 3 minus x when x is greater than or equal to 2.

1. The limit does not exist.

2. 1

3. 2

4. 5

Answer 1

The correct option is 1.

Explanation:

The given function is

`f(x)=\begin{cases}x+3 & \text{ if } x<2 \\ 3-x & \text{ if } x\geq 2 \end{cases}`

We need to find the
`lim_(x\rightarrow 2)f(x)`.

The limit of a function exist if the left hand limit is equal to the right hand limit.

`L=lim_(x\rightarrow a^-)f(x)=lim_(x\rightarrow a^+)f(x)`

Left hand limit:

`LHL=lim_(x\rightarrow 2^-)f(x)`

`LHL=lim_(x\rightarrow 2^-)x+3`

Apply limit.

`LHL=2+3=5`

Right hand limit:

`RHL=lim_(x\rightarrow 2^+)f(x)`

`RHL=lim_(x\rightarrow 2^+)3-x`

Apply limit.

`RHL=3-2=1`

`5\\eq 1`

Since LHL≠RHL, therefore the limit does not exist. Option 1 is correct.

Answer 2

Option 1.

The limit does not exist.

Explanation:

The function is

`f(x) = \left \{{{x+3\ \ \ if\ \ \ x<2} \atop{3-x\ \ \ \ if\ \ \ x\geq2}} \right.`

We seek to find

`\lim_(x \to 2)f(x)`

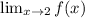
Then we must find the limits on the right of 2 (
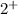`2 ^+`) and on the left of 2 (
`2 ^ -`)

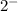If both limits exist and are equal then the
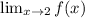`\lim_(x \to 2)f(x)` exists, if both limits are different or do not exist then the
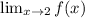`\lim_(x \to 2)f(x)` does not exist.

Limit on the left of 2

`\lim_(x \to 2^-)x+3 = (2) +3 =5\\\\ \lim_(x \to 2^-)x+3 =5`

Limit on the rigth of 2

`\lim_(x \to 2^+)3-x = 3-(2) = 1\\\\ \lim_(x \to 2^+)3-x =1`

Note that both limits give different results. The limit of f(x) when x tends to 2 on the left is equal to 5, and the limit of f(x) when x tends to 2 on the rigth is equal to 1.

Then the
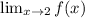`\lim_(x \to 2)f(x)` does not exist.