Answer: Option D.
Explanation:
The Standard form of the equation of then line is:

Where A, B and C are integers.
The Point-slope form of the equationof the line is:

Where m is the slope of the line and (
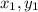 ) is a point of the line.
) is a point of the line.
Given the points (4,2) and (8,1), you can find the slope with the formula
 . Then:
. Then:

Substitute the slope and the point (4,2 ) into
 :
:

To write in Standard form, move the variables to one sides of the equation. Then:
