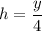Question

A cylinder and a cone have the same volume. The cylinder has radius x and height y. The cone has a radius 2x. Find the height of the cone in terms of y.

Answer 1

The volume of a cylinder is given by

`V=\pi hr^2`

Whereas the volume of a cone is given by

`V=(1)/(3)\pi hr^2`

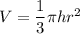
Since the cylinder has radius x and height y, its volume is

`V = \pi x^2y`

And since the cone has a radius 2x, its volume is

`V = \pi (2x)^2 h = 4\pi x^2h`

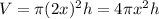
where h is the height of the cone.

We know that the two volumes are the same, so we can build the equation and solve it for h:

`\pi x^2y = 4\pi x^2h`

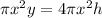
Simplify
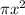`\pi x^2` from both sides:

`y = 4h`

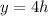
Divide both sides by 4:

`h = (y)/(4)`