Answer:
C. vertical compression
Explanation:
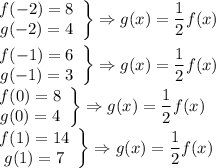
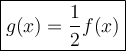
f(x - b) - shifted b units to the right
f(x + b) - shifted b units to the left
f(x) + b - shifted b units up
f(x) - b - shifted b units down
f(-x) - reflected across the y -axis
-f(x) - reflected across the x -axis
f(nx) - a horizontal compression by a factor of n
f(x/n) -a horizontal stretch by a factor of n
nf(x) - a vertical stretch by a factor of n
f(x)/n - a vertical compression by a factor of n