Combining the terms into one fraction, we have
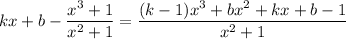
If this converges to 0 as
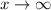 , then the degree of the numerator must be smaller than the degree of the denominator.
, then the degree of the numerator must be smaller than the degree of the denominator.
To ensure this, take
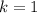 and
and
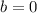 . This eliminates the cubic and quadratic terms in the numerator, and we do have
. This eliminates the cubic and quadratic terms in the numerator, and we do have
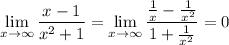
Alternatively, we can compute the quotient and remainder of the rational expression.
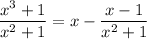
Then in the limit, we have

Both terms on the left vanish if
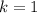 and
and
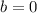 .
.