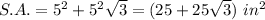Question

Please someone what is the total surface area of this pryamid ​

Answer 1

`\large\boxed{C.\ (25+25\sqrt3)\ in^2}`

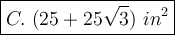
Explanation:

We have the square and four equilateral triangles.

The formula of an area of a squre:

`A_S=a^2`

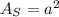
a - length of side

The formula of an area of an equilateral triangle:

`A_T=(a^2\sqrt3)/(4)`

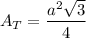
a - length of side

Clculate the areas:

SQURE:

`A_S=x^2\ in^2`

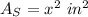
TRIANGLE:

`A_T=(x^2\sqrt3)/(4)\ in^2`

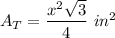
The SURFACE AREA of a square pyramid:

`S.A.=A_S+4A_T\\\\S.A.=x^2+4\cdot(x^2\sqrt3)/(4)=x^2+x^2\sqrt3`

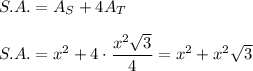
Put x = 5:

`S.A.=5^2+5^2\sqrt3=(25+25\sqrt3)\ in^2`