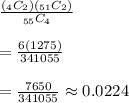Question

If we sample from a small finite population without​ replacement, the binomial distribution should not be used because the events are not independent. If sampling is done without replacement and the outcomes belong to one of two​ types, we can use the hypergeometric distribution. If a population has A objects of one​ type, while the remaining B objects are of the other​ type, and if n objects are sampled without​ replacement, then the probability of getting x objects of type A and nminusx objects of type B under the hypergeometric distribution is given by the following formula. In a lottery​ game, a bettor selects four numbers from 1 to 55 ​(without repetition), and a winning four​-number combination is later randomly selected. Find the probabilities of getting exactly two winning numbers with one ticket.​ (Hint: Use Aequals4​, Bequals51​, nequals4​, and xequals2​.) ​P(x)equalsStartFraction A exclamation mark Over left parenthesis Upper A minus x right parenthesis exclamation mark x exclamation mark EndFraction times StartFraction B exclamation mark Over left parenthesis Upper B minus n plus x right parenthesis exclamation mark left parenthesis n minus x right parenthesis exclamation mark EndFraction divided by StartFraction left parenthesis Upper A plus Upper B right parenthesis exclamation mark Over left parenthesis Upper A plus Upper B minus n right parenthesis exclamation mark n exclamation mark EndFraction

Answer 1

0.0224

Explanation:

The formula for a hypergeometric probability is

`((_AC_x)(_BC_(n-x)))/(_NC_n)`

where A is the number of objects of type A, B is the number of objects of type B, N is the population size, n is the sample size, and x is the number of successes.

for this problem, N is 55. A is the number of objects pulled, which is 4. B is the remaining objects, which is 55. n is the sample size, which is 4, and x is 2:

`((_4C_2)(_(51)C_2))/(_(55)C_4)\\\\=(6(1275))/(341055)\\\\=(7650)/(341055) \approx 0.0224`