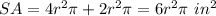Question

A right cylinder has a radius of r inches and height of 2r inches.

In terms of r, the lateral area of the cylinder is ____ r2π square inches.
The area of the two bases together is ____ r2π square inches.
The total surface area of the cylinder is ____ r2π square inches.

Answer 1

its 4, 2, 6 on ed

Explanation:

Answer 2

Part a) The lateral area is
`4r^(2) \pi \ in^(2)`

Part b) The area of the two bases together is
`2r^(2) \pi\ in^(2)`

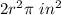
Part c) The surface area is
`6r^(2) \pi\ in^(2)`

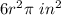
Explanation:

we know that

The surface area of a right cylinder is equal to

`SA=LA+2B`

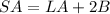
where

LA is the lateral area

B is the area of the base of cylinder

we have

`r=r\ in`

`h=2r\ in`

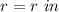
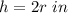
Part a) Find the lateral area

The lateral area is equal to

`LA=2\pi rh`

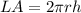
substitute the values

`LA=2\pi r(2r)`

`LA=4r^(2) \pi\ in^(2)`

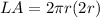
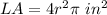
Part b) Find the area of the two bases together

The area of the base B is equal to

`B=r^(2) \pi\ in^(2)`

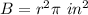
so

the area of the two bases together is

`2B=2r^(2) \pi\ in^(2)`

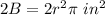
Part c) Find the surface area of the cylinder

`SA=LA+2B`

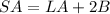
we have

`LA=4r^(2) \pi\ in^(2)`

`2B=2r^(2) \pi\ in^(2)`

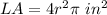
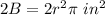
substitute

`SA=4r^(2) \pi+2r^(2) \pi=6r^(2) \pi\ in^(2)`