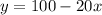Question

The initial cost of an office fax machine is $100. After 1 year, its value becomes $80. Which is the correct linear depreciation model?

Answer 1

`y=100-20x`

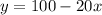
Explanation:

Let the x-axis be the time (in years) and the y-axis the value of the fax machine (in dollars).

We know that the initial value of the fax machine is $100; in other words, when the time is zero years, the value is $100, or as an ordered pair (0, 100). We also know that after 1 year the value decreases to $80, so (1, 80).

Now we can find the slope of the line passing through those two points using the slope formula

`m=(y_2-y_1)/(x_2-x_1)`

where

`m` is the slope

`(x_1,y_1)` are the coordinates of the first point

`(x_2,y_2)` are the coordinates of the second point

Replacing values:

`m=(80-100)/(1-0)`

`m=-20`

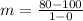
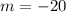
Now, to complete our model we are using the point slope formula

`y-y_1=m(x-x_1)`

where

`m` is the slope

`(x_1,y_1)` are the coordinates of the first point

Replacing values:

`y-100=-20(x-0)`

`y-100=-20x`

`y=-20x+100`

`y=100-20x`

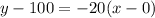
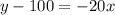
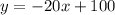
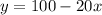
We can conclude that the correct linear depreciation model is
`y=100-20x`