Question

Find the indicated limit, if it exists. limit of f of x as x approaches negative 1 where f of x equals 4 minus x when x is less than negative 1, 5 when x equals negative 1, and x plus 6 when x is greater than negative 1 6 0 5 The limit does not exist.

Answer 1

5

Explanation:

just took the test

Answer 2

The limit is 5

Explanation:

A limit exists if the one-sided limits are equal. So we analyze the limit by approaching it from both the left and the right.

From the left:
`\lim_(x \to \--1) F(x) =  \lim_(x \to \--1) (4-x) = 4-(-1) = 5`

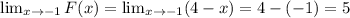
From the right:
`\lim_(x \to \--1) F(x) =  \lim_(x \to \--1) (x+6) = -1+6 = 5`

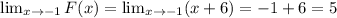
At x= -1 itself: F(x) = 5

Since the limits when approaching from the left and right match, the limit does exist. Thus we conclude that the limit of f of x as x approaches negative 1 is five.