Question

X and Y together can do a piece of work in 10 days and X alone can do it in 15 days would Y alone can finish the work ?​

Answer 1

Y alone can do the piece of work in 30 days.

Explanation:

Proportions

Let's make:

N = days for Y to finish the work alone

Since X alone can do it in 15 days, each day he can do a proportion of 1/15 of the piece of work.

Since Y alone can (possibly) do it in N days, each day he can do 1/N parts of the work.

Together, they do

`\displaystyle (1)/(15)+(1)/(N)`

parts of the work per day. We know they can finish it in 10 days, thus:

`\displaystyle (1)/(15)+(1)/(N)=(1)/(10)`

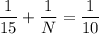
Rearranging:

`\displaystyle (1)/(N)=(1)/(10)-(1)/(15)`

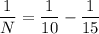
The LCM of 10 and 15 is 30, thus operating:

`\displaystyle (1)/(N)=(3-2)/(30)=(1)/(30)`

Solving for N:

N = 30

Y alone can do the piece of work in 30 days.