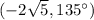Answer:
(5,-5) can be represented in polar form by
 and
and
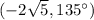
Explanation:
polar coordinates use a distance and an angle
it would be like (x,y) but x is distance from origin to point and y is the angle measured counterclockwise from the positive x-axis.
for (5,-5)
first find the distance to that point using distance formula
distance from (0,0) to (5,-5) is
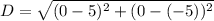
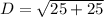
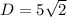
so our point has to be in the form
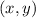 where
where
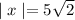
now finding the degree
using inverse tangent
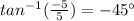
if we look on the graph, it is also 360-45=315 degrees from positive x axis
so one polar coordiante is

the other one is in the oposite side
we add or subtract 180 degrees and make the sign of x negative to go in the oposite direction
subtraction 180 to get 135 degrees
so the other point is
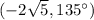
(5,-5) can be represented in polar form by
 and
and