Question

write the inequality that shows the values of xfor which the expression is defined in a square root equation sqrt2x Times Square root x+1?

Answer 1

x ≥ 0

Explanation:

The given expression is:

`√(2x) * √(x+1)`

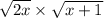
We have to identify for which values of x is the above expression defined. Such values of x constitute the Domain of the function. The rule for square root functions is that the value inside the square cannot be negative, it can be either zero or positive.

The first term is
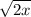`√(2x)`, the value inside the square root will be zero or greater than zero if the value of x is equal to or greater than zero i.e. for x ≥ 0

The second term is
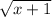`√(x+1)`, the value inside the square root will be zero or greater than zero for x ≥ -1.

Since both these terms are being multiplied, the overall domain will be the intersection of the domains of both terms. i.e. we will only chose those values of x which satisfy both terms.

So, the values of x for which both the terms and thus the overall expression is defined are x ≥ 0