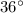Question

The angles in a triangle are such that one angle is 120 degrees more than the smallest angle, while the third angle is 3 times as large as the smallest angle. Find the measures of all three angles.

Answer 1

The measures of the angles are

`132\°`,
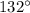`12\°` and
`36\°`

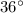
Explanation:

Let

x-----> one angle

y----> the smallest angle

z----> the third angle

we know that

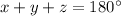`x+y+z=180\°` -----> equation A

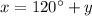`x=120\°+y` ----> equation B

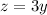`z=3y` -----> equation C

substitute equation B and equation C in equation A and solve for y

`(120\°+y)+y+3y=180\°`

`5y+120\°=180\°`

`5y=180\°-120\°`

`y=60\°/5=12\°`

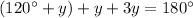
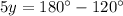
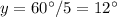
Find the measure of x

`x=120\°+12\°=132\°`

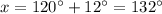
Find the measure of z

`z=3(12\°)=36\°`

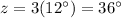
therefore

The measures of the angles are
`132\°`,
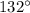`12\°` and
`36\°`