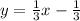Answer:
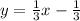
Explanation:
THe slope intercept form of a line is y = mx + b
Where, m is the slope with formula

and
b is the y-intercept (the point where the line cuts the y-axis)
x_1 and y_1 is the first pair of points
x_2, y_2 is the second pair of points
Let's find m first by plugging in the points:
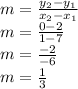
Now we have y = 1/3x+b. We can plug in any point (let's use (1,0)) and find b:

THus, the equation of the line is