Question

Determine the standard form of the equation of the line that passes through 6,-9 and -8,6

Answer 1

15x + 14y = -36

Answer 2

15x + 14y = -218

Explanation:

To write the equation of a line when given two points, calculate the slope and substitute it into the point slope form of a line. From this form of the equation, you can simplify and convert to the standard form.

First, find the slope using the formula.

`m = (y_2-y_1)/(x_2-x_1) =(6--9)/(-8-6) =(15)/(-14)`

Substitute m = -15/14 and the point (-8,6) into the point slope form
`(y-y_1) = m(x-x_1)`.

`y-6=(-15)/(14)(x--8)\\y - 6 = (-15)/(14)(x+8)\\14y + 98 = -15(x + 8)\\14y + 98 = -15x - 120\\15x + 14y + 98 = -120\\15x + 14y = -218`

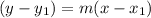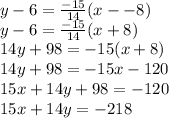
To convert to standard form, multiply the equation by 14. This means each term is multiplied by 14 to clear the denominator. Then multiply using the distributive property. You will now need to move terms across the equal sign. Begin by adding 15x to both sides. Lastly, subtract 98 from both side.