Question

The area of a circle is 42 pi M squared. what is the area of a 60° sector of this circle​

Answer 1

7π square meter

Explanation:

We will use the formula for the area of a sector of a circle which is given by:

`Area = \frac { \theta } { 360 ^ { \circ } } * \pi r^2`

Where
`\theta` is the angle subtended by the sector at the center of the circle. Also, we know that in our case,
`\theta=60^(\circ)`.

Substituting the given values in the formula to get:

`A=(60^(\circ))/(360^(\circ))* 42\pi =(1)/(6)* 42 \pi =7 \pi`

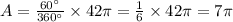
Therefore, the correct answer is 7π square meter.

Answer 2

7π M squared

Explanation:

Since a whole circle is 360°, and we need to find 60° of this circle, we are basically wanting to find
`(60)/(360)=(1)/(6)`th of the circle.

Area is given as 42π M squared, so 1/6th of that is
`(1)/(6)*42\pi\\=7\pi`

THus, the area is 7π M squared