Answer:
Base = 8 cm
Explanation:
We are given that the height of a triangle is 7 cm longer than its base and its area is 60 cm squared.
We are to find the base of the triangle.
Area of the triangle =
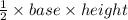
Assuming the base to be
 , so height will be
, so height will be

Substituting the values in the above formula to get:
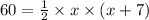
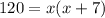
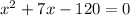
Factorizing the quadratic equation to get:
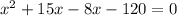
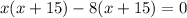

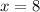 and
and
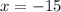
Since base cannot be negative so it will be 8 cm.