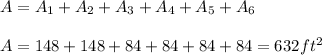Question

What is the surface area of this figure?

Answer 1

632 FT 2 (pretend is small and u know in the right place)

Explanation:

Answer 2

`\boxed{A=632ft^2}`

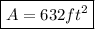
Explanation:

This is a solid because it is a three-dimensional shape. In fact, this solid is a prism for it has two identical bases that has the form of the letter L. The surface area of a solid is the total area of its outer surface. To compute the surface area of this object we must find the area of each face. It's easy to do this by looking at each side of the figure. This is shown in the figure below, therefore:

IN THE DIRECTION 1:

Here we have a face in the form of L, so we can calculate the area by cutting the face in one rectangle and one square. Keep in mind that the area of a rectangle is
`L_(1) * L_(2)` and for a square
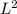`L^(2)`. Therefore:

`A_(1)=8(8)+(14-8)(14)=148ft^2`

IN THE DIRECTION 2:

Here we have the same face as in the direction 1. Accordingly:

`A_(1)=A_(2)=148ft^2`

IN THE DIRECTION 3:

Here we see two rectangles, the first one has dimensions
`8ft \ and \ 6ft[\tex] and the second one [tex](14-8)ft \ and \ 6ft`. Therefore, in this direction we have:

`A_(3)=8(6)+(14-8)(6)=84ft`

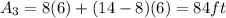
IN THE DIRECTION 4:

Here we see one rectangle of dimensions
`14ft \ and \ 6ft`:

`A_(4)=14(6)=84ft`

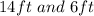IN THE DIRECTION 5 and 6:

Perhaps you noticed that the areas in the directions 5 and 6 are the same just as occurred with 3 and 4, hence we'll calculate the easier area, which is in the direction of 6. Here we have one rectangle of dimensions
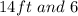`14ft \ and \ 6`. So:

`A_(5)=A_(6)=14(6)=84ft`

Finally, the surface area of the figure is the sum of all the areas of the corresponding directions:

`A=A_(1)+A_(2)+A_(3)+A_(4)+A_(5)+A_(6) \\ \\ A=148+148+84+84+84+84=632ft^2`