Question

4x + 5y = 10

Ax + By = 16
Find a value for A and B that would make the system above have infinitely
many solutions.

Answer 1

For A = 32/5 and B = 8 the system of equations will have infinitely many solutions.

Explanation:

Given equations are:

4x + 5y = 10

Ax + By = 16

The general form of linear equation in two variables is given by:

`ax+by = c`

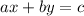
Here a, b and c are constants and x,y are variables.

In the given equations, after comparing with the general form

`a_1 = 4\\b_1 = 5 \\c_1 = 10\\a_2 = A\\b_2 =B\\c_2 = 16`

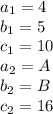
"In order for a system of equations to have infinity many solutions,

`(a_1)/(a_2) = (b_1)/(b_2) = (c_1)/(c_2)` "

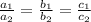Putting the values we get

`(4)/(A) = (5)/(B) = (10)/(16)\\(4)/(A) = (5)/(B) = (5)/(8)\\Now\\(4)/(A) = (5)/(8)\\(A)/(4) = (8)/(5)\\A = (8)/(5) * 4\\A = (32)/(5)\\And\\(5)/(B) = (5)/(8)\\(B)/(5) = (8)/(5)\\B = 8`

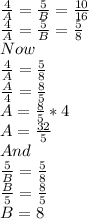
Hence,

For A = 32/5 and B = 8 the system of equations will have infinitely many solutions.