Answer:
The equation of the parabola is
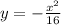
Explanation:
We start by assuming a general point on the parabola
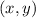 .
.
Using the distance formula
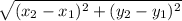 ,
,
we find that the distance between
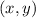 and the focus (0,-4) is
and the focus (0,-4) is
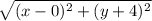 , and the distance between
, and the distance between
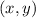 and the directrix y =4 is
and the directrix y =4 is
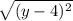 . On the parabola, these distances are equal:
. On the parabola, these distances are equal:
