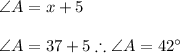Question

What is the measure of 37
42
55
138

Answer 1

42

Explanation:

To solve this problem, we must know two things:

1. The angles of every quadrilateral always add up to 360 degrees.

2. For a quadrilateral whose four corners, or vertices, are all on the same circle, two opposite angles in the cyclic quadrilateral add up to 180 degrees, meaning they are supplementary.

Therefore, we can find two equations and solve this problem:

FROM 1:

Suppose the angle ∠C = y, then it is true that:

`(x+5)+2x+(3x-5)+y=360 \\ \\ \boxed{6x+y=360}`

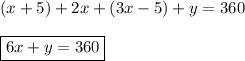
FROM 2:

`x+5+y=180 \\ \\ \boxed{x+y=175}`

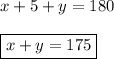
Therefore we need to solve this system of linear equations:

`\left \{ {{6x+y=360} \atop {x+y=175}} \right.`

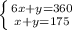
Subtracting 2 from 1:

`5x=185 \\ \\ \therefore x=37`

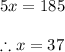
So:

`\angle A=x+5 \\ \\ \angle A=37+5 \therefore \angle A=42^(\circ)`