Answer:
According to this description the area
 of the disc is:
of the disc is:
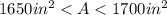
On the other hand, the area of a circumference is given by the following equation:
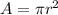 (1)
(1)
Where
 is the radius.
is the radius.
If we want to know the possible lengths of
 for the circular disc, we will have to apply equation (1) for both areas:
for the circular disc, we will have to apply equation (1) for both areas:
For
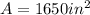 :
:
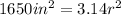
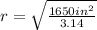
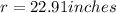
For
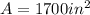 :
:

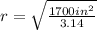
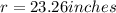
Therefore the radius could be 22.91 inches or 23.26 inches