Answer:

Explanation:
We are given the following function and we are to find the inverse of this function:
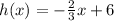
For that, we will put the function equal to another variable
 and make
and make
 the subject of the function.
the subject of the function.
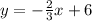
Making
 the subject:
the subject:
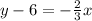

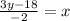

Therefore, the inverse h'(x) =
 .
.