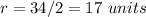Answer:
The length of the radius of the circle K is
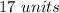
Explanation:
we know that
The triangle CDE is a right triangle with the 90 degree angle at point E
so
Applying the Pythagoras Theorem
Find the length of CD (diameter of the circle K)
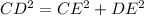
substitute the values
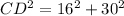
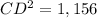
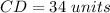
Find the radius
Remember that the radius is half the diameter
so