Question

Evaluate using
Definite integrals

Answer 1

Since
`[0,4]=[0,1]\cup(1,4]`, we can rewrite the integral as

`\displaystyle \int_0^1f(t)\;dt + \int_1^4 f(t)\; dt`

Now there is no ambiguity about the definition of f(t), because in each integral we are integrating a single part of its piecewise definition:

`\displaystyle \int_0^1f(t)\;dt = \int_0^11-3t^2\;dt,\quad \int_1^4 f(t)\; dt = \int_1^4 2t\; dt`

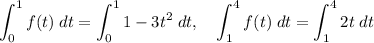
Both integrals are quite immediate: you only need to use the power rule

`\displaystyle \int x^n\;dx=(x^(n+1))/(n+1)`

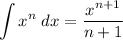
to get

`\displaystyle \int_0^11-3t^2\;dt = \left[t-t^3\right]_0^1,\quad \int_1^4 2t\; dt = \left[t^2\right]_1^4`

Now we only need to evaluate the antiderivatives:

`\left[t-t^3\right]_0^1 = 1-1^3=0,\quad \left[t^2\right]_1^4 = 4^2-1^2=15`

So, the final answer is 15.